• 学术相关
  • Modelling cognitive load using drift-diffusion models in pedestrian street-crossing: a method supported by neural evidence
    • SPL
    • H
    • 模型
    • 实验
    • ROF
  • Debt targets and fiscal consolidation in a euro area HANK model
    • 概述
    • 模型
    • 家庭部门
    • 金融部门
    • 企业部门
    • 政府部门
    • 国际资产演化
    • 联盟的货币政策
    • RoW
    • 出清市场条件
  • Why do product prices affect review ratings? Evidence from a japanese online travel agency
  • Diffusion in social networks: Experimental evidence on information sharing vs persuasion
  • How Algorithms Constrain Consumer Experience

学术相关

Modelling cognitive load using drift-diffusion models in pedestrian street-crossing: a method supported by neural evidence ¹

这篇文章对DDM的一些用法我觉得有点奇怪，不确定是否严谨

SPL

$TTA$为车辆到达时间

Basic perception-based model

$\begin{aligned}dx_p&=P(t)dt+dW\\ P(t)&=\alpha(TTA(t)-\theta_{crit}) \end{aligned}$

Basic utility-based model

$\begin{aligned}dx_u(t)&=\int_t^{TTA_0}U(t’)dt’+dW\\ U(t)&=tanh(U-C(t))\\ C(t)&=\begin{cases}k_c/(TTA_0-t)&,t\leq TTA_0\\ 0&,t>TTA_0\end{cases}\end{aligned}$

H

• H1: influencing evidence model

假设认知负载影响对证据的感知响应

• H2: separate evidence model

假设认知负载直接影响决策，与感知证据无关

• H3: noise model

假设认知负载影响决策噪声变量

模型

对三种假设和2类模型交叉设计：6种模型

① Influencing evidence model $\times$ Perception based framework

$\begin{aligned}P(t)=(\alpha+k_{cog}X_{cog})(TTA(t)-\theta_{crit})\\ X_{cog}=\begin{cases}0&, baseline\\ 1&, cognitive task \end{cases}\end{aligned}$

② Influencing evidence model $\times$ Utility-based framework

$U(t)=tanh((1+k_{cog}X_{cog})(U-C(t)))$

• $k_{cog}$ 量化认知任务的影响

③ Separate evidence model $\times$ Perception-based framework

$P(t)=\alpha(TTA(t)-\theta_{crit})+k_{cog}X_{cog}$

④ Separate evidence model $\times$Utility-based framework

$U(t)=tanh(U-C(t)+k_{cog}X_{cog})$

• $X_{cog}$

⑤ Noise model $\times$ Perception-based framework & Utility-based framework

噪声方差$1+k_{cog}X_{cog}$

边界条件使用坍塌边界

$b(t)=\pm b_0\times\frac{1}{1+e^{-k(TTA_0-t-\tau)}}$

• $k$ 为边界对TTA的敏感性

• $\tau$ 对应（边界半衰期）TTA的特定值，该值处决策边界恰好为 $\pm \frac{1}{2b_{0}}$

非决策时间

$t_{ND}\in N(\mu_{ND},\sigma_{ND})$

拟合方法

PyDDM

• Perception-based model 估计参数： $\alpha,\theta_{crit},k_{cog},b_0,k,\tau,\mu_{ND},\sigma_{ND}$

• Utility-based model 估计参数： $U,k_c,k_{cog},b_0,k,\tau,\mu_{ND},\sigma_{ND}$

损失函数：最大对数似然

模型评价：AIC

实验

$4(TTA)\times2(cognitive\ task\ condition)$

被试：25人（视力正常+戒酒处理）

G*Power方法确定样本量：假设Cohen’s d=0.5，alpha level = 0.05，目标效用 0.95-> 样本量大于23人

实验持续90min，回报为20英镑礼品券，伦理批准

刺激物：Unity生成的高仿真3D场景

60Hz刷新率

处理：

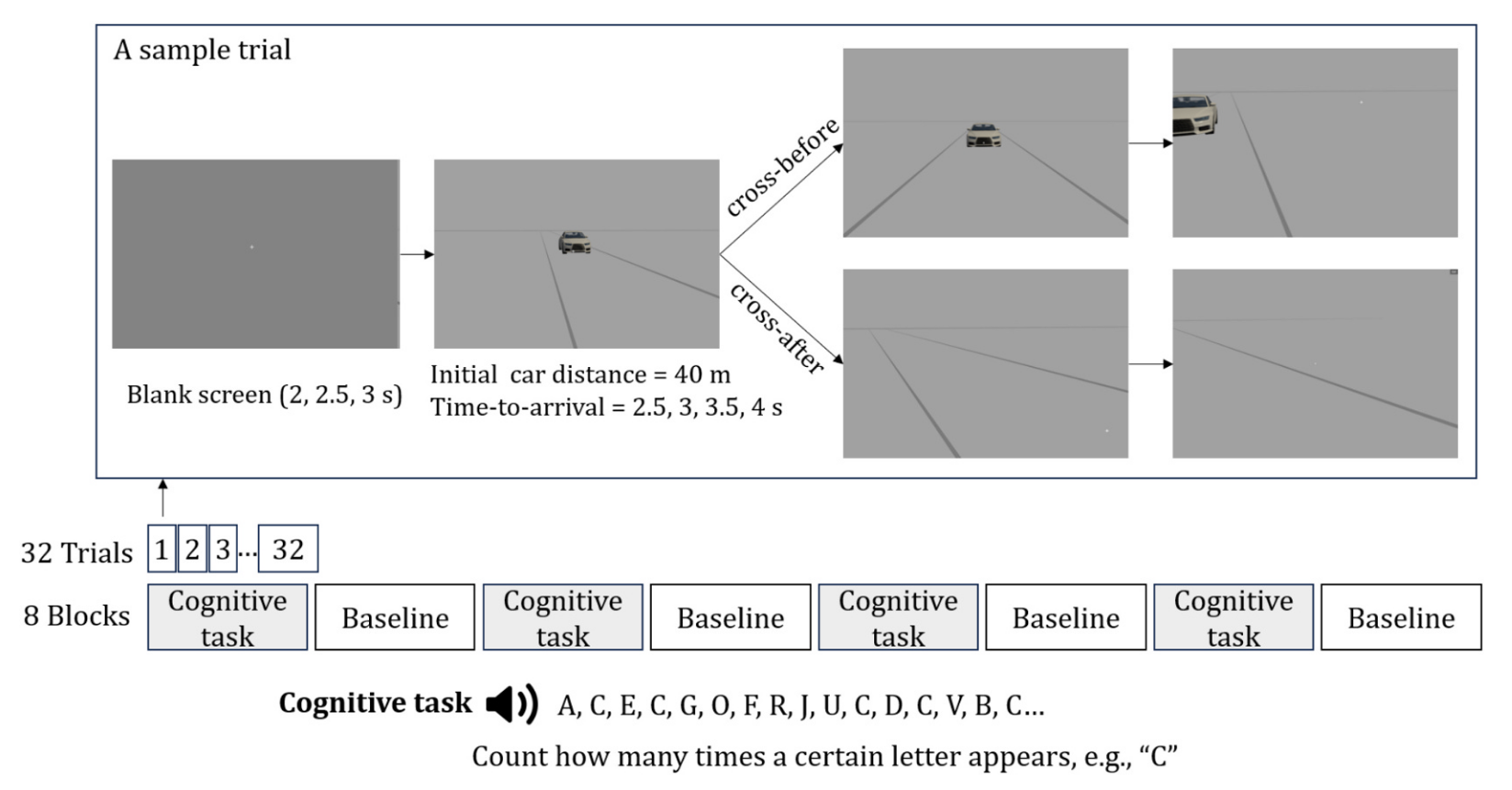
• 测量变量

  • Biosemi ActiveTow system记录EEG：64-channel 10-20 international cap and 6 additional electrodes - 1024Hz样本率记录

    • ActiTools软件降采样至256Hz

  • 决策前穿越频率、响应时间、碰撞概率

• TTA条件

  • 2.5,3,3.5,4s间隔时间

    • 车速16m/s, 13.33m/s, 11.42m/s, 10m/s

• 4.2m宽马路，被试决定过马路，过马路速度1.6m/s

• 实验由8个模块组成，模块在有认知任务和无认知任务之间交替进行

  • 认知任务为统计音频中特定字母出现的次数

结果：

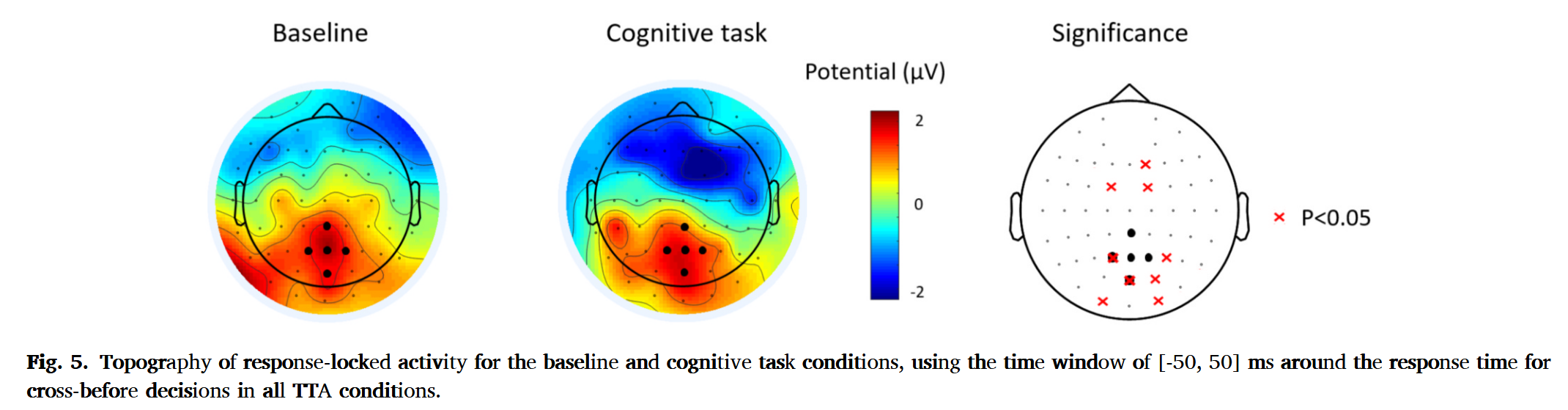
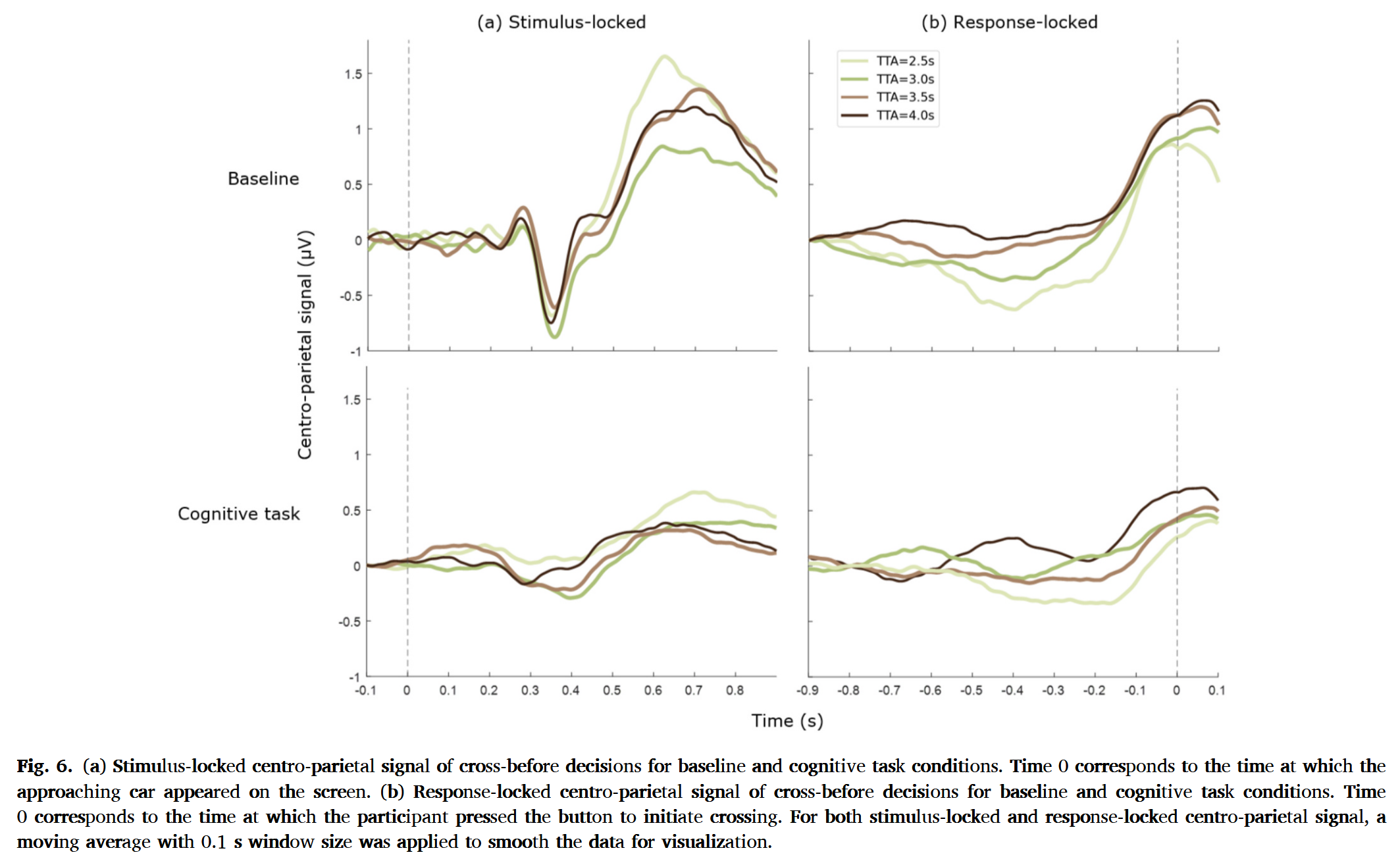
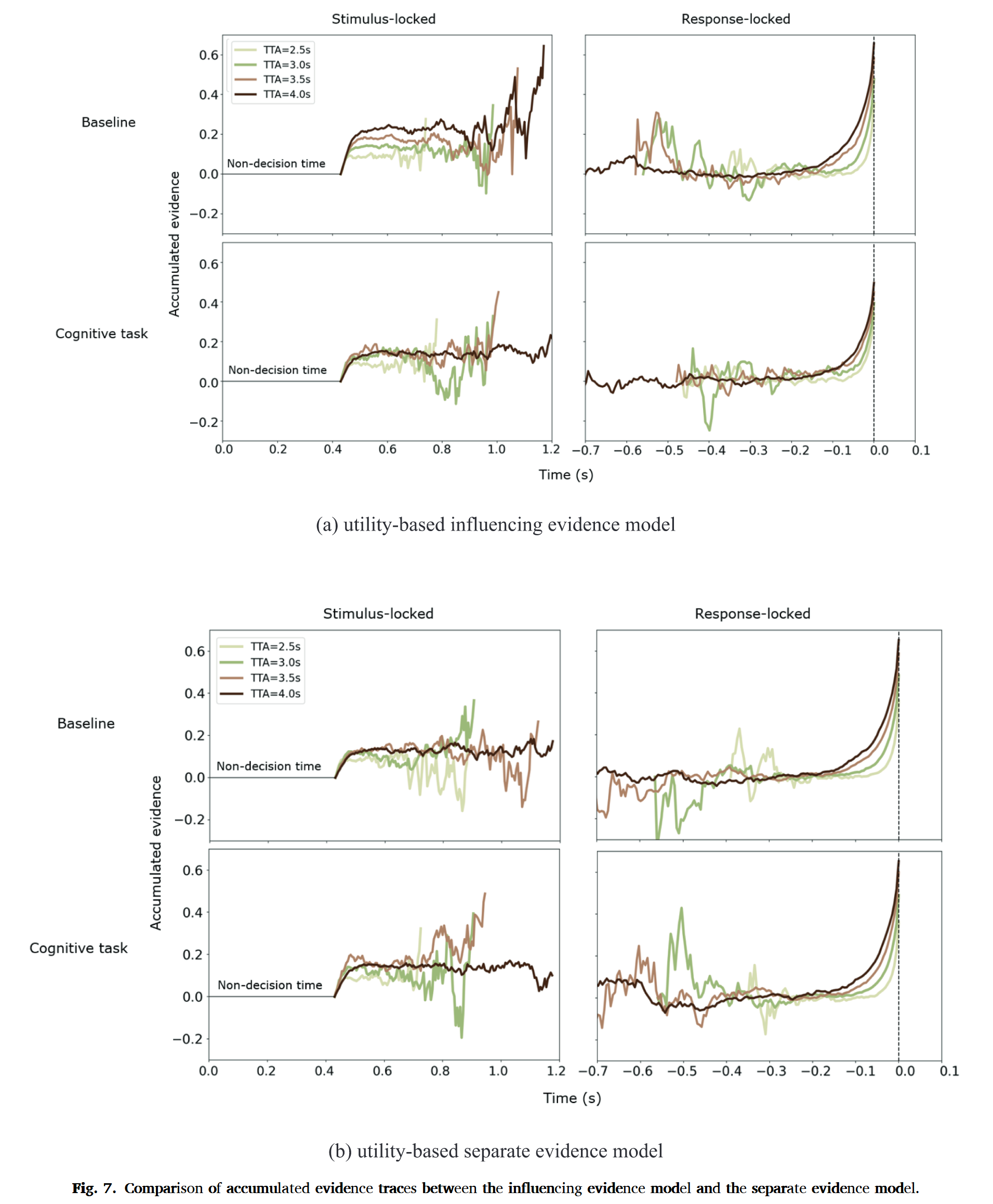
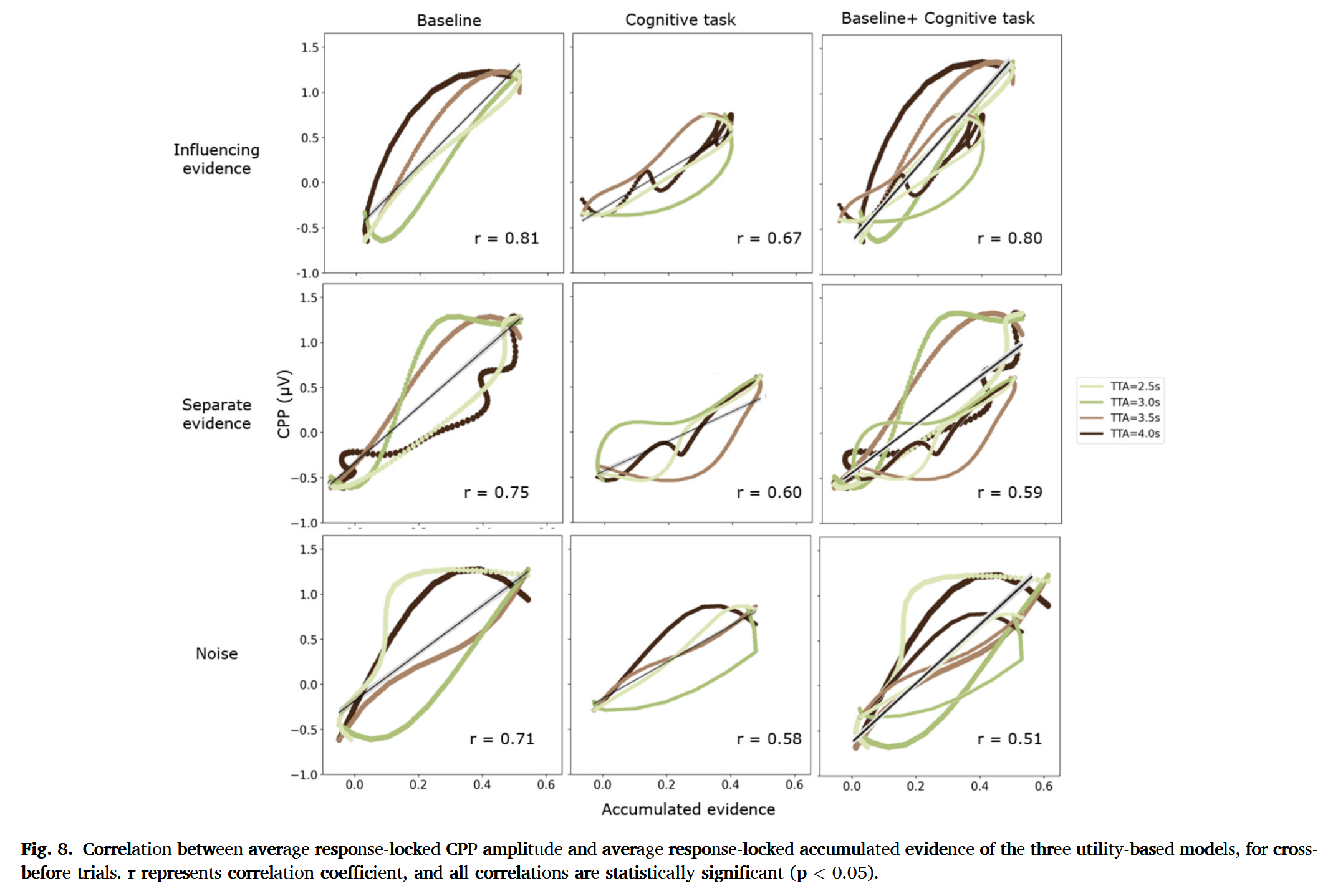
ROF

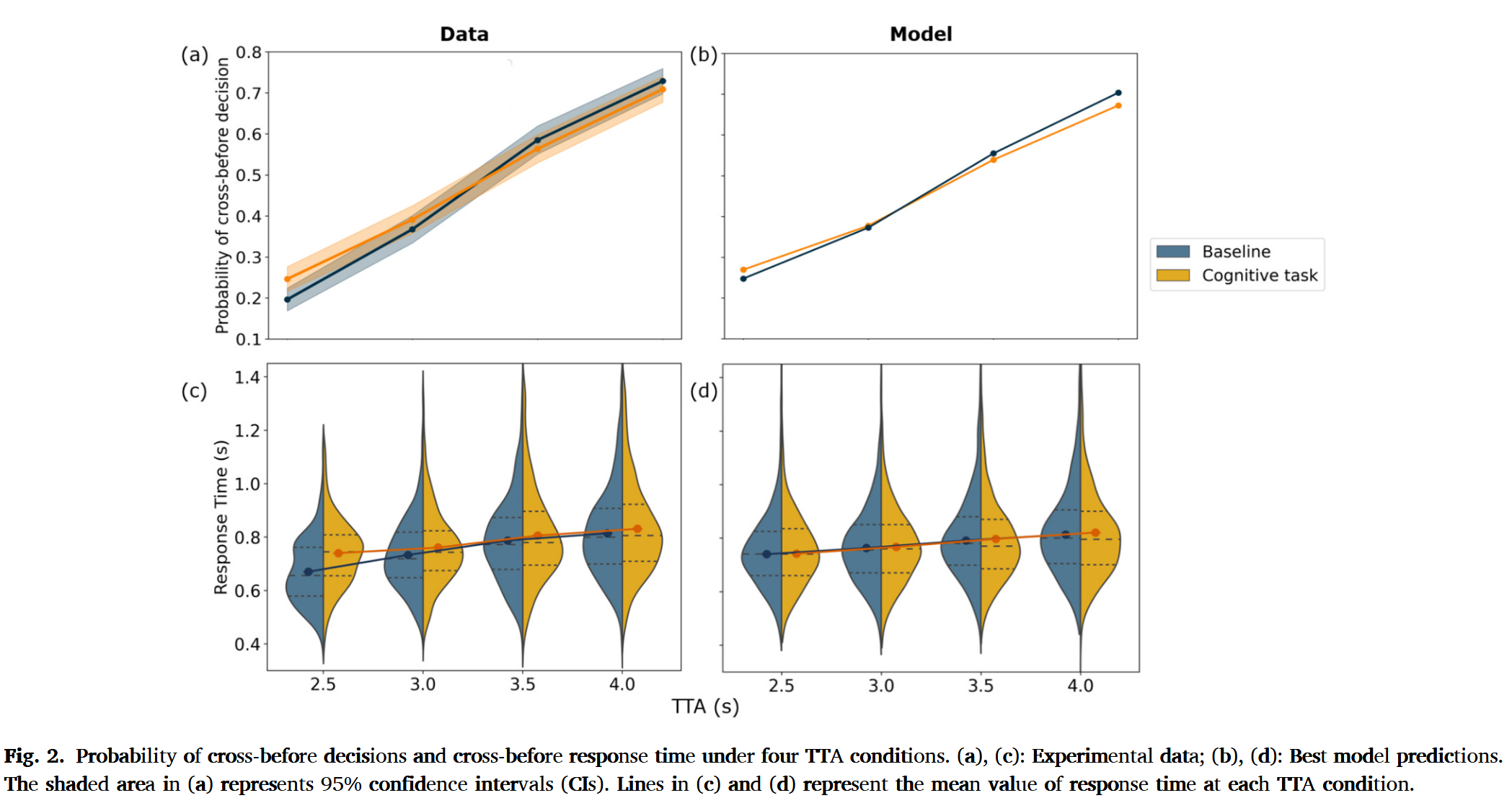
• 认知负荷减弱了汽车抵达时间对过马路决策概率的影响
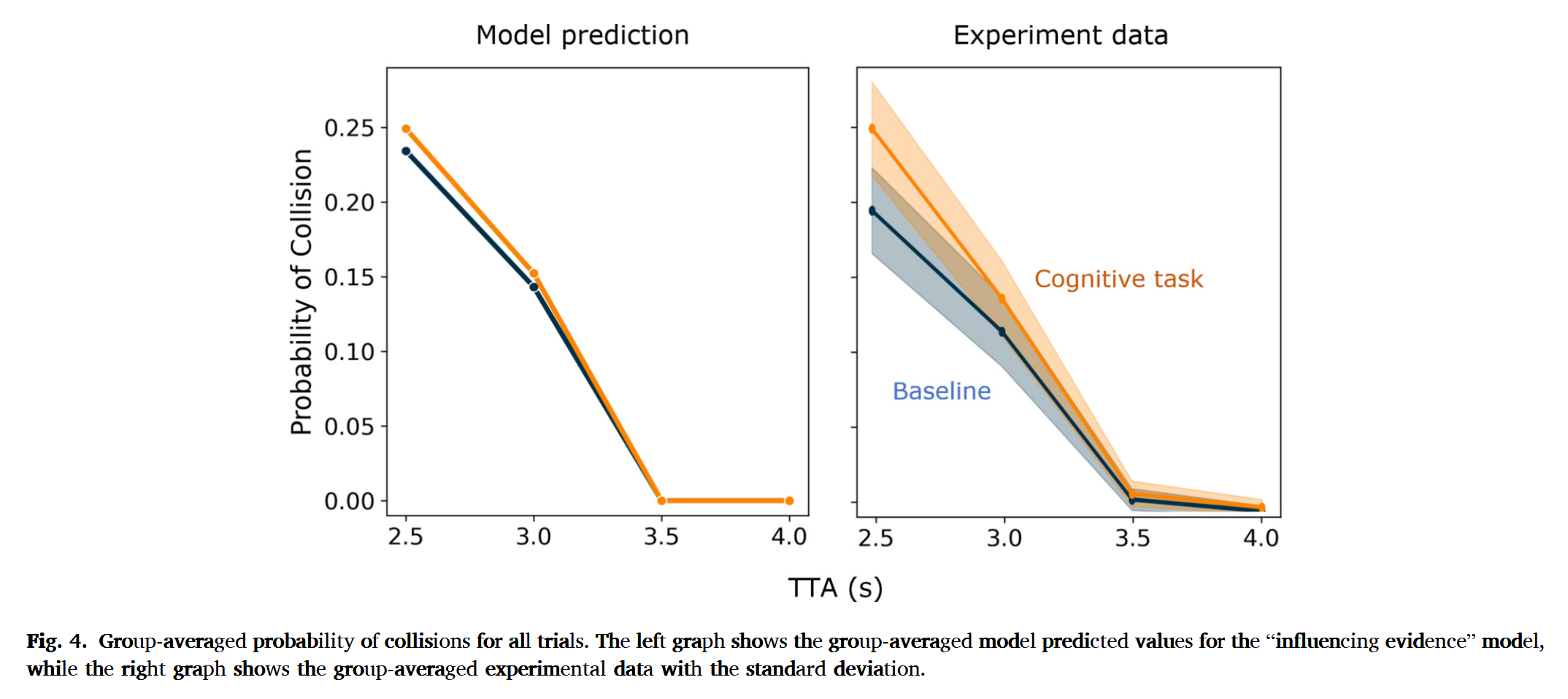
• 认知负荷任务导致反应时间延长，碰撞概率升高
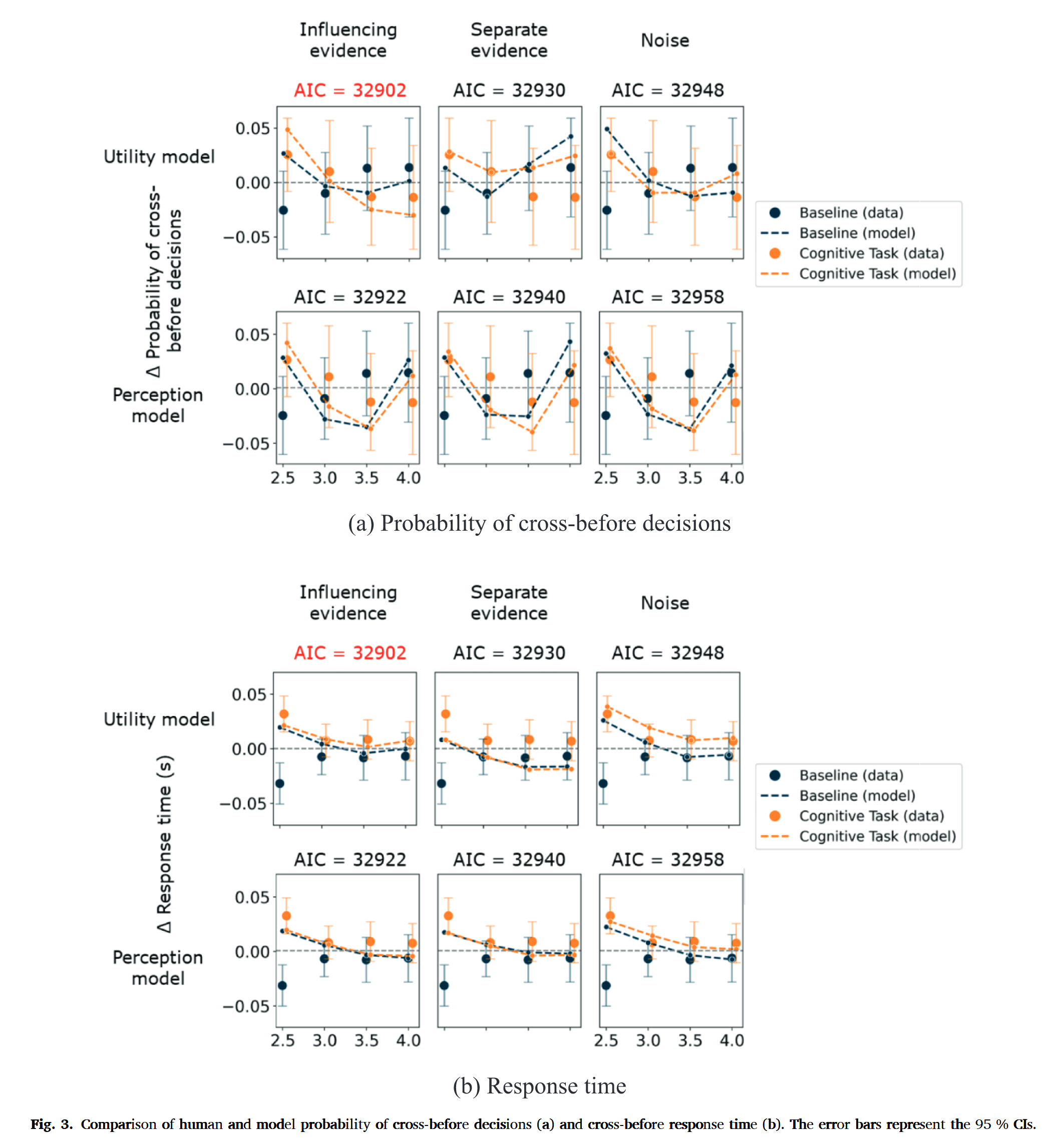
• Influencing evidence $\times$ Utility-based framework 模型效果最佳
• 过马路并非完全自动化行为，需要一定程度的认知控制
• 模型通常高估了响应时间和碰撞风险的感知
• 认知负荷的影响使顶中央区正电位（Centro-Parietal Positivity, CPP）振幅相较基准条件兼容，可能反映了行人过马路任务中注意力的重新分配——由过马路为主转向并向认知任务
• 最佳模型的证据积累与CPP中观察到的衰减模式一致
  • 随着个体收集证据做出决策，CPP会增加，衰弱表明单位时间内证据积累较少

Debt targets and fiscal consolidation in a euro area HANK model ²

这篇研究涉及很多宏观模型，这方面积累不够，读起来比较吃力

次贷危机和新冠大流行这些危机的累积影响使欧洲联盟的公共债务水平创历史新高，远超《马斯特里赫特条约》（MT）和《稳定增长公约》（SGP）设定的60%参考值

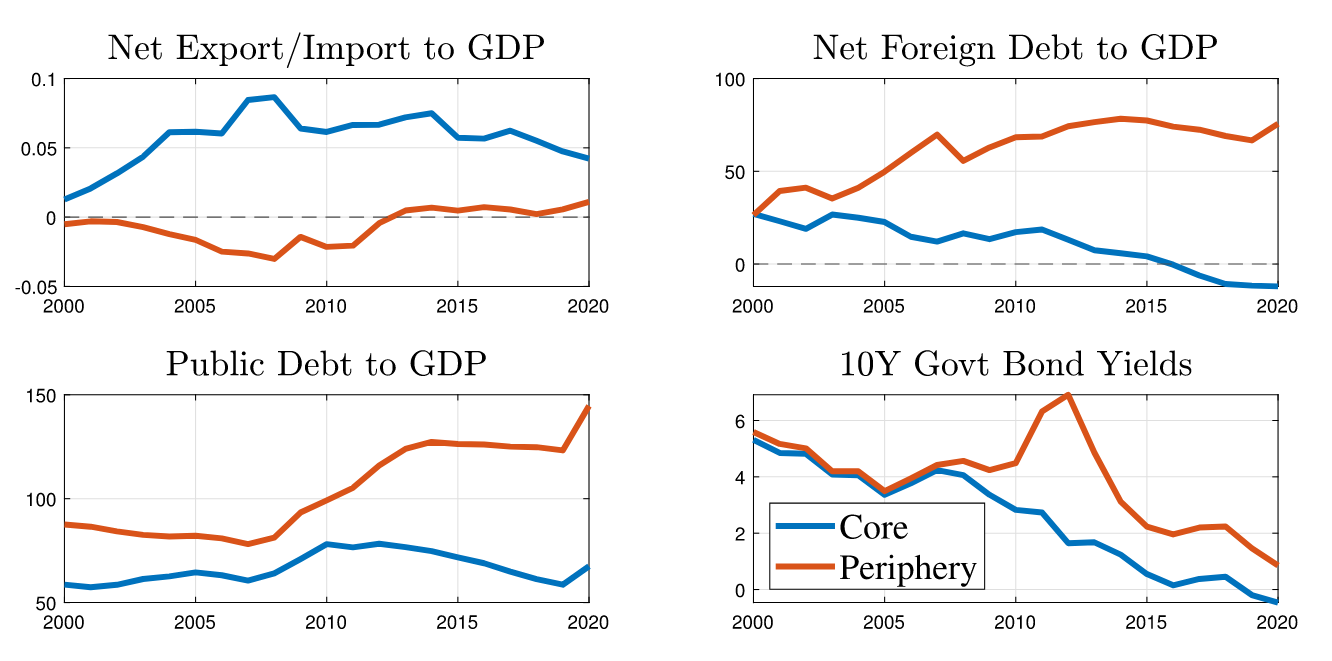
欧盟Core-Periphery地区存在经济不平衡，这些不平衡导致近期的全球危机对不同成员国具有不同的影响

核心区指奥地利、德国和荷兰的GDP加权平均值；边缘区指西班牙、意大利、葡萄牙和希腊的GDP加权平均值

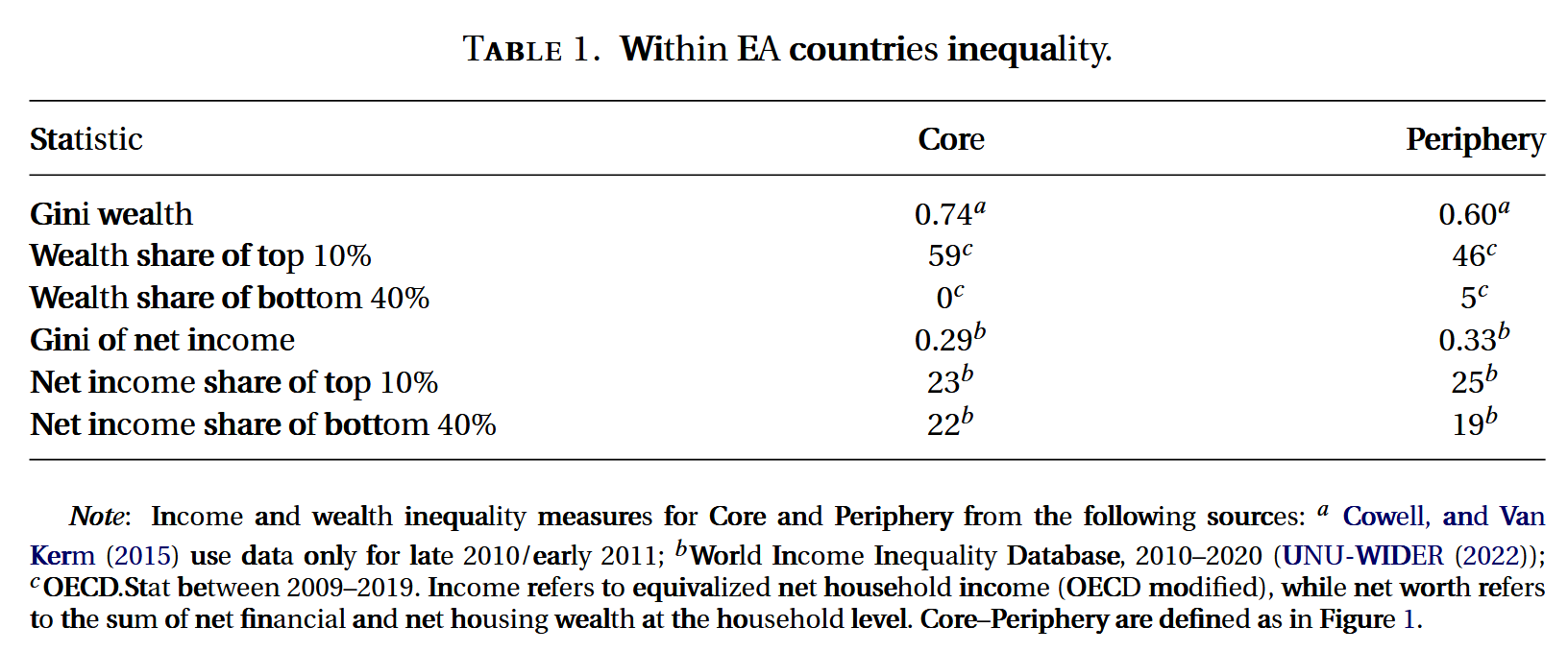
边缘区持续表现出较低的财富不平等和更高的收入不平等

概述

模型包含两个国家和世界其他地区RoW，每个国家由多个异质性家庭、企业、共同基金和国家政府组成。金融市场不完整，满足à la Bewley–Huggett–Aiyagari (BHA) 范式

BHA 范式

• 不完全市场+不可保个体风险

  • 家庭无法通过金融合约完全对冲个体层面的收入冲击

• 异质性主体+连续财富分布

• 借贷约束+预防性贮蓄

• 稳态分布

  • BHA 范式的均衡并非 “代表性主体的最优决策 + 宏观变量均衡”，而是「个体最优决策、市场出清、财富分布稳态」三者的一致性 —— 即宏观变量（利率、工资）与财富分布相互影响、相互决定，最终达到 “不随时间变化” 的稳态

两个国家相互贸易并同RoW贸易，每个国家都以主权溢价向RoW借贷，这种溢价对净外债具有弹性（自己和另一个国家）

两国确定双边名义汇率，单一货币当局根据泰勒规则设定名义汇率，假设国家财政政策独立

该模型对标2000-2019年欧盟核心区与边缘区

基准财政场景符合《马斯特里赫特条约》参考值（公共债务产出比率降至60%），称为财政形式Fiscal Formality (FF)

将债务目标调整为100%，反映了当前欧盟横截面平均水平，称为经济现实Fiscal Realism (FR)

考察核心区的财政扩张能否促进边缘区的财政整合，允许核心区增长它们的债务目标为100%，边缘区降低至100%，称为经济调节Fiscal Accommodation (FA)

结果

FF情境中国内与国际成本均高，且成本在国家和家庭之间分布不均，边缘区相对贫困的家庭遭受了最高的福利损失

若欧盟将债务目标调整到FR，能够显著减轻两国各阶层家庭的福利损失，同时抑制财富不平等统计数据的上升

若允许核心区扩张，边缘区坚守FA将导致核心区家庭与绝大多数边缘区家庭之间产生利益冲突

研究结果表明优化后的欧盟债务产出目标介于两国SQ债务产出比之间，即67%-145%

根据基准校准，优化债务目标为120%

模型

两个国家是等体积的，经济结构是对称的

其他国家RoW使用简约形式，使用 $\tilde{}$ 标注

本国称为核心区，外国称为边缘区使用$^\ast$标注

家庭部门

偏好与消费束

采用消费 - 闲暇可分离的 CRRA 效用函数，消费带来的正效用与闲暇带来的正效用相互独立

每个家庭$h$对消费$c_{h,t}$和工作小时$l_{h,t}$使用终身效用$\mathbb{E}_0\sum_{t=0}^{\infty}\beta^t(c_{h,t}^{1-\sigma}/(1-\sigma)-\varphi l_{h,t}^{1+\eta}/(1+\eta))$，其中$\beta\in(0,1)$是家庭主观贴现因子，$\sigma$为跨期替代弹性的倒数，$\frac{1}{\eta}$为劳动力供给的Frisch弹性，$\varphi >0$是劳动负效用的相对权重

消费篮$c_{h,t}$是核心区$c_{H,h,t}$，边缘区$c_{F,h,t}$和其他国家$c_{RoW,h,t}$的常替代弹性的聚合

$c_{h,t}=[(\chi^H)^{\frac{1}{\theta}(c_{H,h,t})^{\frac{\theta-1}{\theta}}}+(\chi^F)^{\frac{1}{\theta}}(c_{F,h,t})^{\frac{\theta-1}{\theta}}+(1-\chi^H-\chi^F)^{\frac{1}{\theta}}(c_{RoW,h,t})^{\frac{\theta-1}{\theta}}]^{\frac{\theta}{\theta-1}}$

其中参数$\theta>0$是三种贸易商品之间的替代弹性，$\chi^H,\chi^F,1-\chi^H-\chi^F$表示核心区、边缘区和RoW产品权重

每个家庭选择$c_{H,h,t}, c_{F,h,t},c_{RoW,h,t}$消费来最小化总消费支出，产出对三种贸易商品的需求函数

$c_{H,h,t}=\chi^H[\frac{P_{H,t}}{P_t}]^{-\theta}c_{h,t},\quad c_{F,h,t}=\chi^F[\frac{P_{F,t}}{P_t}]^{-\theta}c_{h,t},\quad c_{RoW,h,t}=(1-\chi^H-\chi^F)[\frac{P_{RoW,t}}{P_t}]^{-\theta}c_{h,t}$

其中$P_t=[\chi^H(P_{H,t}^{1-\theta}+\chi^F(P_{F,t})^{1-\theta}+(1-\chi^H-\chi^F)(P_{RoW,t})^{1-\theta}]^{\frac{1}{1-\theta}}$为核心区消费者价格指数

核心商品在边缘区销售$P_{H,t}=S_tP_{H,t}^\ast$，在RoW为$P_{H,t}\tilde{S}t\tilde{P}_{H,t}$，其中$P_{H,t}^\ast$和$\tilde{P}_{H,t}$是以边缘区和RoW货币计的核心区产品名义价格，$S_t,\tilde{S}_t$为名义汇率，以核心区货币每单位对边缘区/RoW计

核心区与边缘区的货币联盟使$S_t$保持一致，$\tilde{S}_t$表示货币联盟和RoW的名义汇率

核心区与边缘区、RoW的真实汇率为$Q_t\equiv\frac{P_t^\ast}{P_t}$，$\tilde{Q}_t\equiv\frac{\tilde{S}_t\tilde{P}_t}{P_t}$，其中$P_t^\ast,\tilde{P}_t$表示边缘区和RoW的总价格水平

家庭生产力与收入过程

工资收入$w_t\varepsilon_{h,t}l_{h,t}$，其中$w_t\equiv\frac{W_t}{P_t}$表示真实工资率，$\varepsilon_{h,t}$表示异质性生产力，$l_{h,t}$为家庭劳动供给，利润$d_t$根据家庭异质生产力分享

家庭劳动力总收入为$w_t\varepsilon_{h,t}l_{h,t}+\varepsilon_{h,t}d_t$

假设异质生产力过程$\varepsilon_{h,t}$遵循增强型m状态马尔可夫链，即马尔可夫链中具有一个“常规”部分遵循离散化的对数正态AR(1)过程，持久性参数$\rho$方差$\sigma_{\varepsilon}^2$，同时增加两个额得状态，一个捕获超高生产力，另一个捕获低生产力家庭

状态空间$\varepsilon=[\bar{\varepsilon}_1,\cdots,\bar{\varepsilon}_\ell,\cdots,\bar{\varepsilon}_m,\bar{\varepsilon}_p,\bar{\varepsilon}_r]$，其中前$m$元素对应常规状态，$\ell$对应中间状态；$\bar{\varepsilon}_p=\frac{\bar{\varepsilon}_1}{2}$和$\bar{\varepsilon}_r=\bar{\varepsilon}_m^2$分别代表低和高生产力状态

增强型马尔可夫链转移矩阵$\left [ \begin{array}{c|c} \underset{m \times m}{\Gamma_{\varepsilon \varepsilon’}} & \underset{m \times 2}{\Gamma_{\varepsilon z}} \\ \hline \underset{2 \times m}{\Gamma_{z \varepsilon’}} & \underset{2 \times 2}{\Gamma_{z z’}}\end{array}\right]\equiv \left[ \begin{array}{ccccc|cc} p_{11’} p_z & \dots & p_{1 \ell’} p_z & \dots & p_{1 m’} p_z & p_p & p_r \\ \vdots & \ddots & \vdots & \ddots & \vdots & \vdots & \vdots \\ p_{m 1’} p_z & \dots & p_{m \ell’} p_z & \dots & p_{m m’} p_z & p_p & p_r\\ \hline 0 & \dots & 1 - p_{p p’} & \dots & 0 & p_{p p’} & 0 \\ 0 & \dots & 1 - p_{r r’} & \dots & 0 & 0 & p_{r r’}\end{array}\right ]$

其中$p_z+p_p+p_r=1$

$\underset{m \times m}{\Gamma_{\varepsilon \varepsilon’}}$子矩阵包含转移概率$p_{\iota,\iota’}$，其中$\iota,\iota’=1,\cdots,m$表示从常规状态$\varepsilon_\iota$到$\varepsilon’_{\iota’}$的转移概率

矩阵$\underset{m,2}{\Gamma_{\varepsilon z}}=J_{\underset{m,1}{m,1}}\times[\underset{1,2}{p_p,p_r}]$其中$J_{m,1}$为全1矩阵，$p_p,p_r$表示家庭从$m$常规状态转向低生产力和高生产力状态的概率

$\underset{2\times2}{\Gamma_{zz’}}$包含表示保留在低生产力和高生产力状态的概率$p_{pp’},p_{rr’}$

子矩阵$\underset{2\times m}{\Gamma_{z\varepsilon’}}$包含互补概率$(1-p_{pp’})$和$(1-p_{rr’})$表示一个家庭退出高/低生产力状态转入常规生产力中间状态$\ell$的概率

假设家庭不能从低-高生产力状态直接转移

马尔可夫链的不变集分布为$\xi$，归一化为$E[\varepsilon_t]=\sum_{\varepsilon\in\mathcal{E}}\varepsilon\xi(\varepsilon)=1$

两个国家的马尔可夫链参数可以存在差异

消费与储蓄选择

假设不完全市场，家庭可以在国内共同基金中储蓄，部分自我保险以抵御特殊冲击，也可以通过欠条部分借贷

假设工作小时数由公会层面决定，即每个家庭$h$工作$l_{h,t}$个小时

给定初始值$a_{h,-1},\varepsilon_{h,0}$，典型家庭$h$选择计划${c_{h,t}}_{t=0}^\infty$和${a_{h,t}}_{t=0}^\infty$解决最大化终身效用问题

$\begin{aligned}V_0(a_{h,-1},\varepsilon_{h,0})&=\underset{{c_{h,t,a_{h,t}}}_{t=0}^\infty}{max}\mathbb{E}_0\sum_{t=0}^\infty\beta^t(\frac{(c_{h,t})^{1-\sigma}}{1-\sigma}-\varphi\frac{(l_{h,t})^{1+\eta}}{1+\eta})\\ s.t.\quad & c_{h,t}+a_{h,t}=R(a_{h,t-1},i_{t-1}^a,\tau_t^a)\frac{P_{t-1}}{P_t}a_{h,t-1}+(1-\tau_t^l)(w_{h,t}\varepsilon_{h,t}l_{h,t}+\varepsilon_{h,t}d_t)^{1-\tau_t^p}\\ &a_{h,t}\geq-\underline{a}_t \ \text{and}\ c_{h,t}\geq 0\end{aligned}$

其中$c_{h,t}$是前文的CES聚合公式

家庭服从税和转移税约束，$\tau_t^p$和$\tau_t^l$决定累进税收和经济平均税收水平

$R(a_{h,t-1},i_{t-1}^a,\tau_t^a)$表示典型家庭面对的税后名义总利息率，家庭有正的净储蓄$a_{h,t-1}>0$，将资产投资到国内共同基金获得名义净回报$i_{t-1}^a$

国家政府对净收益征收$\tau_t^a$的税，税后名义净收益为$(1-\tau_t^a)i_{t-1}^a$

净储蓄为负的家庭$a_{h,t-1}<0$向其他家庭借贷会产生中介成本

国内共同基金支付的利率与欠条支付的利率差为$1+i_{t-1}^a+\Delta$

这种假设会导致大量家庭净储蓄接近0，但可以选择有代价的借款

存在可变的临时借款限额$\underline{a}_t\equiv\lambda\frac{P_{H,t}}{P_t}Y_{H,t}$

工资

家庭向多个公会出售劳动服务，而公会设定名义工资以最大化平均家庭的福利，但面临类似Rotemberg-type调整成本

在对称均衡中，所有公会设定相同工资，所有家庭提供相同工时

该设定产生了一个标准的工资菲利普斯曲线

$ln(1 + \pi^w_t) = \kappa_w \left[ \varphi(L_t)^{1+\eta} - \frac{1}{\mu_w} (1 - \tau^p_t)(1 - \tau^l_t) U_t^{CW} \right] + \beta \ln(1 + \pi^w_{t+1})$

其中$1+\pi_t^w\equiv \frac{W_t}{W_{t-1}}$为工资通胀，$U_t^{CW}\equiv \left( \frac{W_t}{L_t} + d_t \right) - \tau_t^p \frac{W_tL_t}{P_t} \int_h \left[ (\varepsilon_{h,t})^{1 - \tau_t^p} c_{h,t}^{-\sigma} \right] dh$为边际消费的生产率加权总量

金融部门

国际资本流通通过共同基金实现

风险中性的宫廷基金向核心区家庭发行债券，$t$期期末的名义总价值为$P_tA_t=P_t\int_h a_{h,t}dh$，支付名义净收益率$i_t^a$

核心区共同基金可以进入国内外资产市场，投资国内政府债券$P_tB_t$，获取名义利润率$i_{H,t}$，也可以通过Row货币计价的国际资产$\tilde{P}t\tilde{F}t$以名义利率$i_{RoW,t}$向RoW借贷

共同基金的目标是最大化债券$A_t$对应的期望真实回报率$E_t[1+r_t^a]\equiv\frac{1+i_t^a}{1+\pi_{t+1}}$，通过选择投资$B_t$和$\tilde{F}_t$

这推导出$t\geq 1$时期的无套利条件$1+r_t^a=\frac{1+i_t^a}{1+\pi_{t+1}}=\frac{1+i_{RoW,t}}{1+\tilde{\pi}_{t+1}}\frac{\tilde{Q}_{t+1}}{\tilde{Q}_t}=\frac{1+i_{H,t}}{1+\pi_{t+1}}$

其中$1+\pi_{t+1}\equiv \frac{P_{t+1}}{P_t}$为核心区通胀率，$1+\tilde{\pi}_{t+1}\equiv\frac{\tilde{p}_{t+1}}{\tilde{p}_t}$

允许在第0期有资本利得$r_0^a\neq r_{-1}^a$

假设$r_0^a$为国内政府债券和国际资产真实回报率的加权平均

企业部门

存在两类企业，一类是竞争性的最终商品包装商，一类是垄断竞争的中间品企业连续统

最终企业生产核心区的贸易商品$Y_{H,t}=(\int_0^1(Y_{H,j,t})^{\frac{1}{\mu}}dj)^\mu$，使用Dixit-Stiglitz聚合器组合中间品$j$，$\mu$为差异性中间商品的替代弹性

每家中间品公司雇佣劳动力使用线性技术$Y_{H,j,t}=Zn_{j,t}$生产中间品$j$，$Z$为总劳动生产率

它们依据Rotemberg-type调整成本设置价格，公司的优化问题得到一个标准的新凯恩斯菲利普斯曲线

$\ln\left( \frac{1 + \pi_{H,t}}{1 + \pi_H} \right) = \kappa \left( \frac{P_t}{P_{H,t}} \frac{w_t}{Z} - \frac{1}{\mu} \right) + \frac{1}{1 + r_t^a} \frac{Y_{H,t+1}}{Y_{H,t}} \ln\left( \frac{1 + \pi_{H,t+1}}{1 + \pi_H} \right)$

其中$1 + \pi_{H,t}\equiv\frac{P_{H,t}}{P_{H,t-1}}$为核心区产出平减指数的通胀，$\pi_H$为稳定状态通胀率

每家中间企业的实际利润为$d_t=\frac{P_{H,t}}{P_t}Y_{H,t}-w_tN_t-\frac{P_{H,t}}{P_t}\psi_t$，其中$\psi_t$调整成本

政府部门

核心区国家各期政府预算限制为$B_t + \frac{\tau_t^a i_{t-1}^a A_{t-1}^+}{1 + \pi_t} + w_t L_t + d_t - (1 - \tau_t^l) \left(w_t L_t + d_t\right)^{1 - \tau_t^p} E_t=\frac{(1+i_{H,t-1})B_{t-1}}{1+\pi_t}+\frac{P_{H,t}G_{H,t}}{P_t}$

其中$E_{t}\equiv \sum_{\varepsilon\in\mathcal{E}}(\varepsilon_{h,t})^{1-\tau_t^p}\xi(\varepsilon)$，$A_{t-1}^+\equiv\int_h\mathbb{I}_{a_{h,t-1}>0}a_{h,t-1}dh$

税收收入扣除劳动转移支付为$w_tL_t+d_t-(1-\tau_t^l)(w_tL_t+d_t)t^{1-\tau_t^P}E_t$

资本收入的税收为$\frac{\tau_t^ai_{t-1}^aA_t^+}{1+\pi_t}$

$B_t$为期末国内政府债务，向共同基金借贷的名义利率为$i_{H,t}$

政府支持$G_{H,t}$完全分配给国产产品$g_{H,t}\equiv \frac{G_{H,t}}{Y_{H,t}}$

核心区政府劳动收入税为$\tau_t^l=\bar{\tau}^l+\gamma_l(b_{t-1}-\bar{b})$

其中$\bar{\tau}$为税收目标，$\gamma_l\geq 0$为核心区公共债务与产出比的反馈政策系数

$b_{t-1}=\frac{B_{t-1}}{\frac{P_{H,t-1}}{P_{t-1}}Y_{H,t-1}}$，$\bar{b}$为债务目标

国际资产演化

核心区国家的净外资演化

$\widetilde{Q}_t \widetilde{F}_t = ( \frac{1 + i_{\text{RoW}, t-1}}{1 + \widetilde{\pi}_t} ) \widetilde{Q}_t \widetilde{F}_{t-1} + \Delta_{t-1} \frac{P_{t-1}}{P_t} + ( \frac{P_{H,t}}{P_t} C_{H,t}^* - \frac{P_{F,t}}{P_t} C_{F,t} ) + ( \frac{P_{H,t}}{P_t} \widetilde{C}_{H,t} - \frac{P_{\text{RoW},t}}{P_t} C_{\text{RoW},t} )$

其中$\frac{P_{H,t}}{P_t} C_{H,t}^* - \frac{P_{F,t}}{P_t} C_{F,t} \text{和} \frac{P_{H,t}}{P_t} \widetilde{C}_{H,t} - \frac{P_{\text{RoW},t}}{P_t} C_{\text{RoW},t}$为核心区向边缘区和RoW的净出（进）口

联盟的货币政策

两个国家组成一个货币联盟，即双边名义交换率是外生设定的$S_t=1$，因此单一货币机构只能独立设定名义利率之一

$i_{H,t}$和$i_{F,t}^\ast$名义利息率是内生变量

欧盟的中央银行根据Taylor-type利息率规则设置$i_{H,t}$回应欧盟的通胀（核心区$\pi_t$和边缘区$\pi_t^\ast$的CPI通胀率加权平均）

$i_{H,t} = \bar{\iota} + \phi_{\pi} \left( \varsigma(\pi_t - \bar{\pi}) + (1 - \varsigma)(\pi_t^* - \bar{\pi}) \right)$

其中$\bar{\iota}$和$\bar{\pi}$为货币政策目标，$\phi_\pi>1$是欧盟CPI通胀的货币政策反馈系数

$0\leq \varsigma\leq 1$是欧盟央行对核心区的权重，即边缘区对目标的通胀偏离

RoW

商品市场

RoW整体需求$\widetilde{Y}$，价格水平$\widetilde{P}_t$，Row生产的商品价格$\widetilde{P}_{RoW,t}$

联盟价格不影响RoW价格水平

RoW对核心区、边缘区商品需求$\widetilde{C}_{H,t} = \left( \widetilde{P}_{H,t}/\widetilde{P}_t \right)^{-\theta_H} \widetilde{Y}, \ \widetilde{C}_{F,t} = \left( \widetilde{P}_{F,t}/\widetilde{P}_t \right)^{-\theta_F} \widetilde{Y}$以RoW货币计价的核心区和外围去商品价格，价格弹性$\widetilde{\theta}_H,\widetilde{\theta}_F$

核心区、边缘区向RoW以价格$\widetilde{P}_{RoW,t}$进口商品满足$C_{RoW,t}$和$C_{RoW,t}^\ast$

价格$P_{RoW,t}=P_{RoW,t}^\ast=\widetilde{S}_t\widetilde{P}_{RoW,t}$

资本市场

RoW向核心/边缘区共同基金借贷

成员国的国际名义利率具有债务弹性

核心区向RoW的借贷成本$i_{RoW,t}$

$1+i_{RoW,t}=(1+\tilde{\iota})+\zeta{exp[(1-\varpi)(nfd_t-\overline{nfd})+\varpi(nfd_t^\ast-\overline{nfd}^\ast)]-1}$

$nfd_t,nfd_t^\ast$是核心和边缘区的净外债与产出比

核心区的借贷成本是净外债（资产）$nfd_t$相对阈值$\overline{nfd}$的递增（减）函数，也可能取决于边缘区净外债产出比$nfd_t^\ast$对阈值$\overline{nfd}^\ast$

$\zeta>0$为国际名义利率对净外债的弹性

$\varpi\in[0,1)$为直接财政外部性的强度，$\tilde{\iota}$为外生的随时间不变的世界利率成分

出清市场条件

$\begin{aligned}N_t&=L_t\\ A_t&=B_t+\widetilde{Q}_t\widetilde{F}_t\\ Y_{H,t}&=C_{H,t}+C_{H,t}^\ast+\widetilde{C}_{H,t}+G_{H,t}+\psi_t\end{aligned}$

其中$A_t\equiv\int_h a_{h,t}dh, C_{H,t}\equiv\int_hc_{H,h,t}dh$

$C_{H,t}^\ast,\widetilde{C}_{H,t}$为边缘区和RoW对核心区生产商品的需求

Why do product prices affect review ratings? Evidence from a japanese online travel agency ³

Diffusion in social networks: Experimental evidence on information sharing vs persuasion ⁴

How Algorithms Constrain Consumer Experience ⁵

• Previous
  【阅】本周阅读摘选2025-11-10 → 2025-11-16
• Next
  【阅】本周阅读摘选2025-11-24 → 2025-11-30