• 学术相关
  • Algorithmic Precision and Human Decision: A Study of Interactive Optimization for School Schedules
    • Error Analysis
    • 模型
    • 仿真分析
    • 交互优化
    • 交互UI设计
    • 应用
  • Collaborative learning and decision making on pricing and recommendation: a simple framework for planning
  • Proxy-aided demand learning with an application to various pricing problems

学术相关

Algorithmic Precision and Human Decision: A Study of Interactive Optimization for School Schedules ¹

这篇研究的主要贡献是提出了一种将优化问题线性化，进而高效求解的方法，并基于此建立了一种基于抽样构建分布空的辅助决策方法，有些处理比较有意思。

这篇研究具有较强的写作“技术性”，例如使用了大量公式描述与本文核心贡献无关的误差分析，构建“数学墙”，但实际上笔峰一转：“We cannot model the interplay of $ε_{tot}$, $ε_{opt}$, and $ε_{pol}$ in full generality, as they are highly complex and domaindependent.” 此外，作者还使用了多处拉丁语词汇。

Error Analysis

Optimization Error

• 优化问题: 给定政策选择 $\lambda \in \Lambda$

$\begin{aligned}min&\quad c(x,\lambda)\\ s.t.&\quad x\in\chi\end{aligned}$

其中$x\in\chi$表示可行解（即每所学校上下学时间）；$c(x,\lambda)$为解$x$在给定政策$\lambda$下的开销

• 优化误差：研究者贡献通过解 $x$ 的优化误差测量 $\varepsilon_{opt}(x,\lambda)=c(x,\lambda)-c(x^\ast(\lambda),\lambda)$

其中$x^\ast(\lambda)=arg\ min_{x\in\chi}c(x,\lambda)$为给定政策$\lambda$下的优化解

优化误差可能源于模型简化或算力限制

Policy Error

每个政策$\lambda\in\Lambda$表示政策制定者对损失函数$c(\cdot,\lambda)$的选择（例如：最小化交通成本、满足家长/员工偏好、提升学生健康）及其相对重要性

政策硬约束通过无穷大成本表示

理论最优政策选择$\lambda^{true}\in\Lambda$，$c(\cdot,\lambda^{true})$为利益相关者效用损失，$x^{\ast}(\lambda^{true})$为对应最优解

• 政策误差 $\varepsilon_{pol}(\lambda)=c(x^\ast(\lambda),\lambda^{true}) - c(x^\ast(\lambda^{true}),\lambda^{true})$

即给定政策下最优优化成本与最优政策下最优成本的差

协同交互优化

政策制定与研究优化的共同目标是最小化相关利益者效用损失

• 在理想政策 $\lambda^{true}$ 下的总误差 $\varepsilon_{tot}(x)=c(x,\lambda^{true})-c(x^\ast(\lambda^{true}), \lambda^{ture})$

命题1：对任意政策$\lambda$，总误差可以分解

$\varepsilon_{tot}(x)=\varepsilon_{pol}(\lambda)+\varepsilon_{opt}(x,\lambda)+\delta(x,\lambda)$

其中$\delta(x,\lambda)=c(x,\lambda^{true})-c(x,\lambda)$

POC: 很奇怪的设定，既然是总误差，就应该把政策设定作为一个参数；现在在定义中使用$\lambda^{true}$后面又用$\forall \lambda$非常混乱。而且这段推导感觉有问题，若严格按照前文的定义$c(x^\ast(\lambda),\lambda^{true})$与$c(x^\ast(\lambda),\lambda)$消不了。

POC：这段的真实含义："Proposition 1 shows that the total error is not exactly the sum of policy and optimization errors, as captured by δ(x,l)." 前面的所有数学公式均没有实际意义

模型

考虑$N$期模型，每期政策制定者与研究员都会降低各自的误差

对$\forall n\geq 0$，令$\varepsilon_{pol}^n\geq 0$为政策误差，$\varepsilon_{opt}^n$为优化误差

设$\varepsilon_{pol}^0=\varepsilon_{opt}^0=1$

优化目标 $min\quad\varepsilon_{tot}^n$

假设$\varepsilon_{tot}^n=\varepsilon_{pol}^n+\varepsilon_{opt}^n$

政策不变场景

即$\varepsilon_{pol}^n= p$

优化演化$\varepsilon_{opt}^{n+1}=\varepsilon_{opt}^{n}(1-\rho)$

无优化场景

即$\forall n \quad \varepsilon_{opt}^n=0$

演化场景$\varepsilon_{pol}^{n+1}=\gamma_o+(\varepsilon_{pol}^n-\gamma_o)(1-\pi)$即政策误差以$1-\pi$的速率向优化极限$\gamma_o$收敛

其中$\gamma_o$为当前研究者优化水平下的政策收敛极限，若研究者水平突破，该极限会变化

正常场景下$\gamma$为研究依赖系数0

全模型

$\begin{aligned}\varepsilon_{opt}^{n+1}&=\varepsilon_{opt}^n(1-\rho)+(\varepsilon_{pol}^n-\varepsilon_{pol}^{n+1})\\ \varepsilon_{pol}^{n+1}&=\gamma\varepsilon_{opt}^{n}+(\varepsilon_{pol}^{n}-\gamma\varepsilon_{opt}^n)(1-\pi)\end{aligned}$

优化问题会随着政策误差减少拥有更多的优化空间，每次政策优化都会先将问题转移到研究优化上，再由研究优化实现

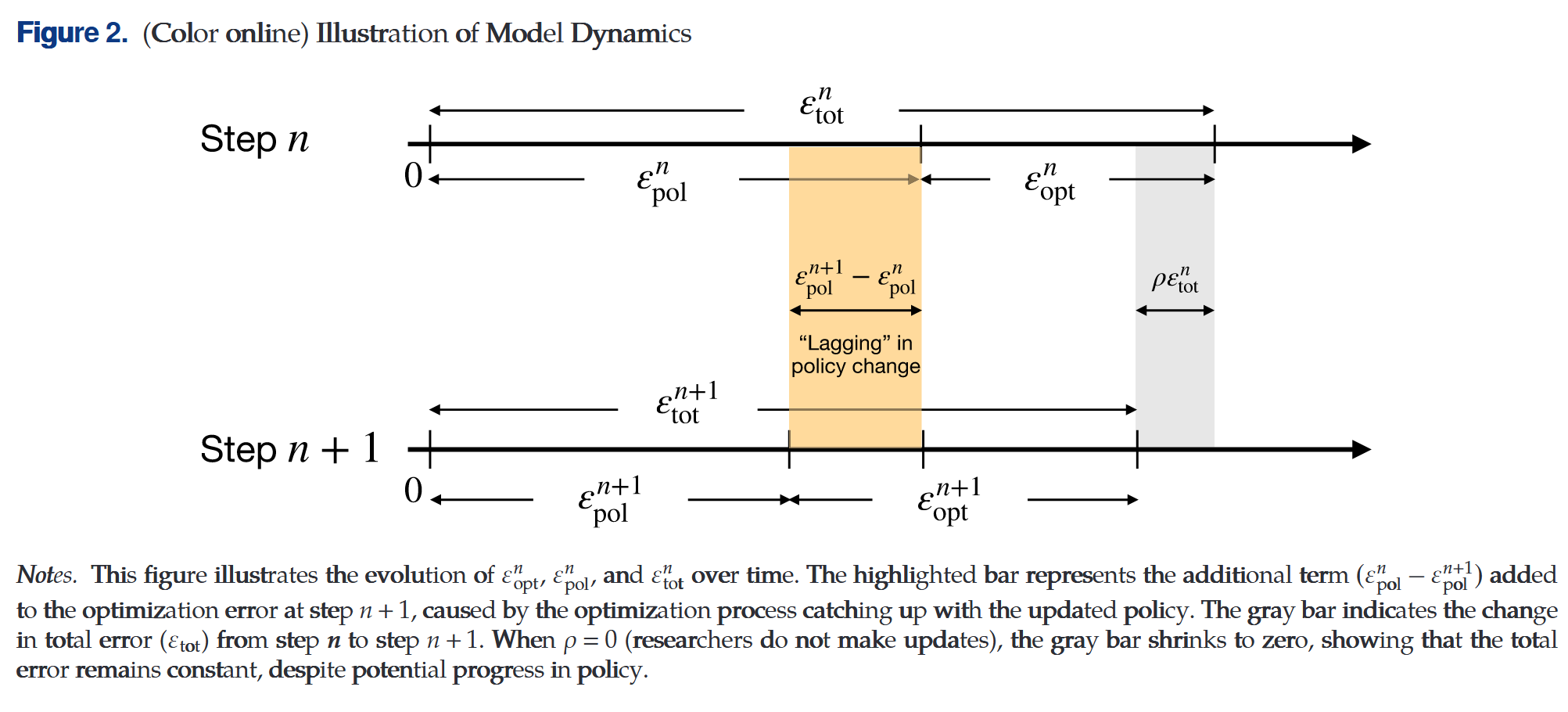
若$\gamma<1, \rho,\pi>0$，当$N\to \infty$时，$\varepsilon_{tot}\to 0$

严格地讲，当$limit N\to\infty$时，有渐进紧确界$\varepsilon_{tot}^N=\Theta((1-\alpha)^N)$

其中通过特征值分析可解$\alpha=\left\{ \begin{aligned}&\frac{\rho+\pi(1+\gamma)}{2}(1-\sqrt{1-\frac{4\pi\rho}{(\rho+\pi(1+\gamma))^2}}),\quad &if\ \gamma>0 \\ &\pi &if\ \gamma=0\end{aligned}\right.$

分析可知$limit_{\gamma\to 0}\alpha=min(\pi,\rho)=\left\{\begin{aligned}\pi,\quad &if\ \rho\geq \pi \\ \rho,\quad &if\ \rho<\pi\end{aligned}\right.$

• 瓶颈效应

若不存在研究依赖，则政策误差的收敛效率为$1-\alpha$，若存在即使是极小的依赖，整体误差的收敛速率都会受政策优化或研究优化中慢的一个影响

• 收敛速度提升

令$k=\frac{\rho}{\pi}$为研究优化与政策优化系数之比，当研究足够快$k\geq \frac{\gamma}{3}$时分析全微分有$-\frac{\partial \alpha}{\partial k}-\frac{\partial \alpha}{\partial \gamma}\geq 0$

即缩小研究-政策优化比和减少研究依赖可以提供整体收敛速率

优化模型

交互系统需要强调响应速度

考虑一组学校索引$1,\cdots, S$和$T$个可能开始时间索引$1,\cdots, T$，第$t$开始时间选项为$h_t$

决策变量使用二元编码：$x_{s,t}=1$当学校$s$在$t$时间上课，否则为0

决策解集矩阵$\chi=\left\{\mathbf{x}\in{0,1}^{S\times T}:\sum_{t=1}^T x_{s,t}=1\ \forall s=1,\cdots, S\right\}$限制每个学校只能有一个上课时间

不失一般性，考虑两个目标

$\begin{aligned}minimize&\quad \lambda_{cost}f_{cost}(x)+\lambda_{change}f_{change}(x)\\ s.t.&\quad x\in\chi\end{aligned}$

其中$f_{cost}(x)$为校车选择时间$x$的成本；$f_{change}$为上课时间与当前状态的总变化；$\lambda_{cost}$与$\lambda_{change}$为它们的优先级权重

两个目标都是非线性的，但后者可以轻易地线性化

$f_{change}(x)=\sum_{s=1}^S|\sum_{t=1}^T h_tx_{s,t}-o_s|$其中$o_s$为学校$s$的原始开课时间

$f_{chaneg}$可以使用至多$S$个辅助变量线性化

线性化

每所学校都会在早晚运行一系列班车，每次运行对应一趟由单一校车停靠的一系列站点，接送学生

$s$学校早班车$r\in{1,\cdots,R_s^{AM}}$从学生站点到学校；晚班车$r\in{1,\cdots, R_s^{PM}}$由学校$s$到学生停靠站

班车运行$r$到学校的耗时为$\delta_{s,r}$

学校$s$上课时间$h_t$，则早班车$r$从$h_t-\delta_{s,r}$运行到$h_t$；相应的晚班车$r’$从$h_t+\ell_s$运行到$h_t+\ell_s+\delta_{s,r}$，其中$\ell_s$指定学校$s$的课程持续时间（分钟）

在时间$\theta$，若该时间在运行的起始时间段之间，则认为该运行是活跃的

则在时间$\theta$的总活跃班数为$\begin{aligned}N_{s,t,\theta}^{AM}&=\sum_{r=1}^{R_s^{AM}}\mathbf{1}(h_t-\delta_{s,r}\leq\theta\leq h_t)\\ N_{s,t,\theta}^{PM}&=\sum_{r=1}^{R_s^{PM}}\mathbf{1}(h_t+\ell_s\leq\theta\leq h_t+\ell_s+\delta_{s,r})\end{aligned}$

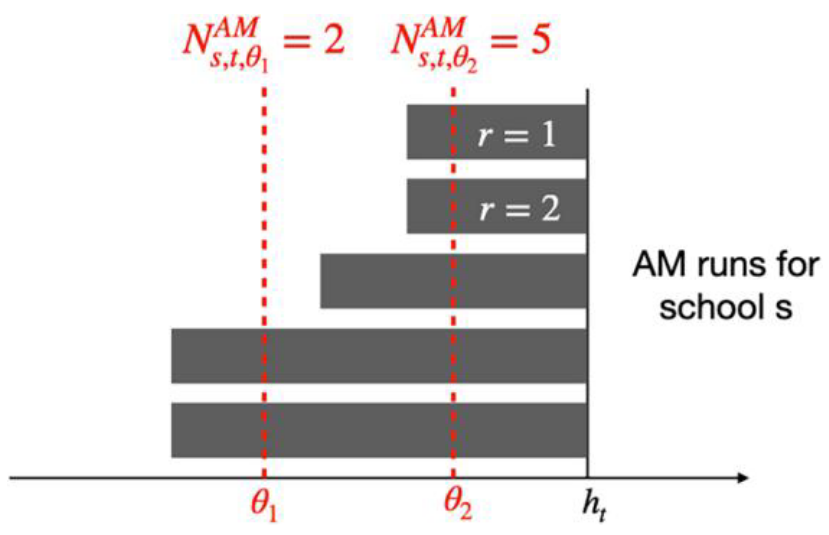
张量$N^{AM}$和$N^{PM}$可以轻松地使用$\theta$离散合集进行预计算，得到$\Theta$

交通成本线性化

交通成本的主体是校车车队规模，一种有效的估算方法是任何时刻最大活跃运行次数

$f_{cost}(x)=max_{\theta\in\Theta}((N_{s,t,\theta}^{AM}+N_{s,t,\theta}^{PM})x_{s,t})$，它可以仅使用一个变量线性化

仿真分析

作者使用Boston Public Schools数据集（134所学校、约2万名学生）作为测试集，与Bertsimas et al. 2019三种方法进行对比
(i) 平衡基线（balanced baseline）：最小化各允许开始时间的最大路线数；
(ii) 随机重启法（random restarts）：随机采样16次后选择最优解；
(iii) 二次分配公式（quadratic assignment formulation）：通过调参优化路线兼容性与开始时间分散性。

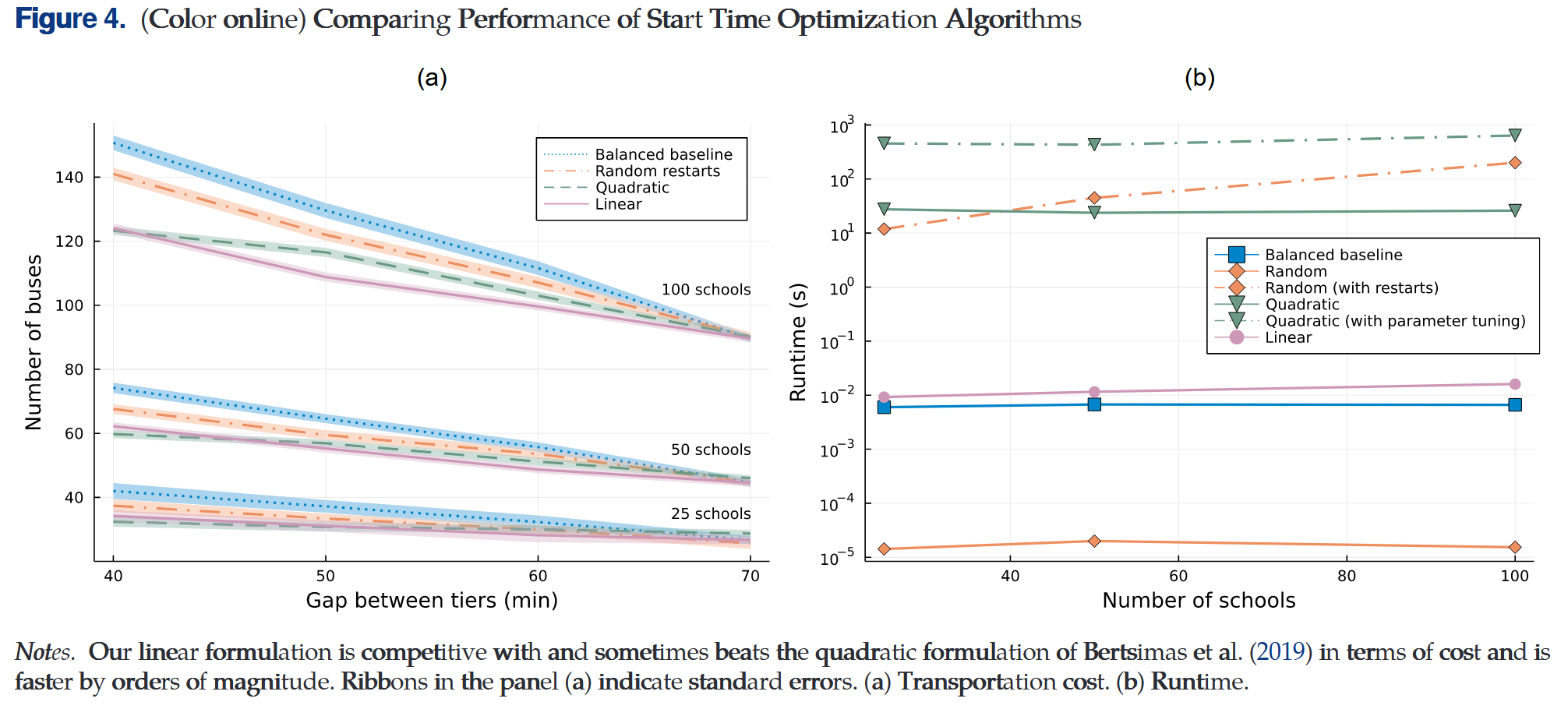
结果表明作者提出的张量线性化方法在运输成本上与表现最佳的二次分配法接近，甚至在某些场景下更优，而计算效率要比二次分配法快约3个量级

结果表明作者提出的线性化算法在未牺牲解质量的前提下，有效地提升了计算效率

交互优化

政策制定者的主要挑战是制定目标优先级，他们通常知晓需要优化的目标

在这样的情况下，经典的方法是计算帕累托最优解，让政策制定者可以将抽象的权重同实际结果联系起来

由于本研究的方法计算效率高，因此可以很好地处理有限目标获得帕累托最优解，让参数在研究者与政策制定者之间交互

次优解空间抽样

为便于产生具象的理解，作者设计了抽样方法来展示参数的多样性和次优解性质

假设政策制定者当前政策偏好为$f^\ast$，给定权重优化目标值$c^\ast=min_{x\in\chi}f^\ast(x)$

随机矩阵$P$元素$P_{s,t}$表示学校$s$对上课时间$t$的偏好分，它从$[0,1]$中独立均匀采样

对每个$P$的实现解优化问题

$\begin{aligned}max_{x\in\chi}&\quad\sum_{s=1}^S\sum_{t=1}^T P_{s,t}x_{s,t}\\ s.t.&\quad f^\ast(x)\leq (1+\gamma)c^\ast\end{aligned}$

其中$\gamma>0$是预算乘数，表示愿意接受的原目标$c^\ast$的最大劣化

随机矩阵展示解的尽可能多样的可能

重复抽样-优化过程$N$次，定义每次抽样$i=1,\cdots,N$的优化解为$x^i$

学校$s$在抽样$i$的上课时间为$H_{i,s}=\sum_{t}x_{s,t}^i h_t$

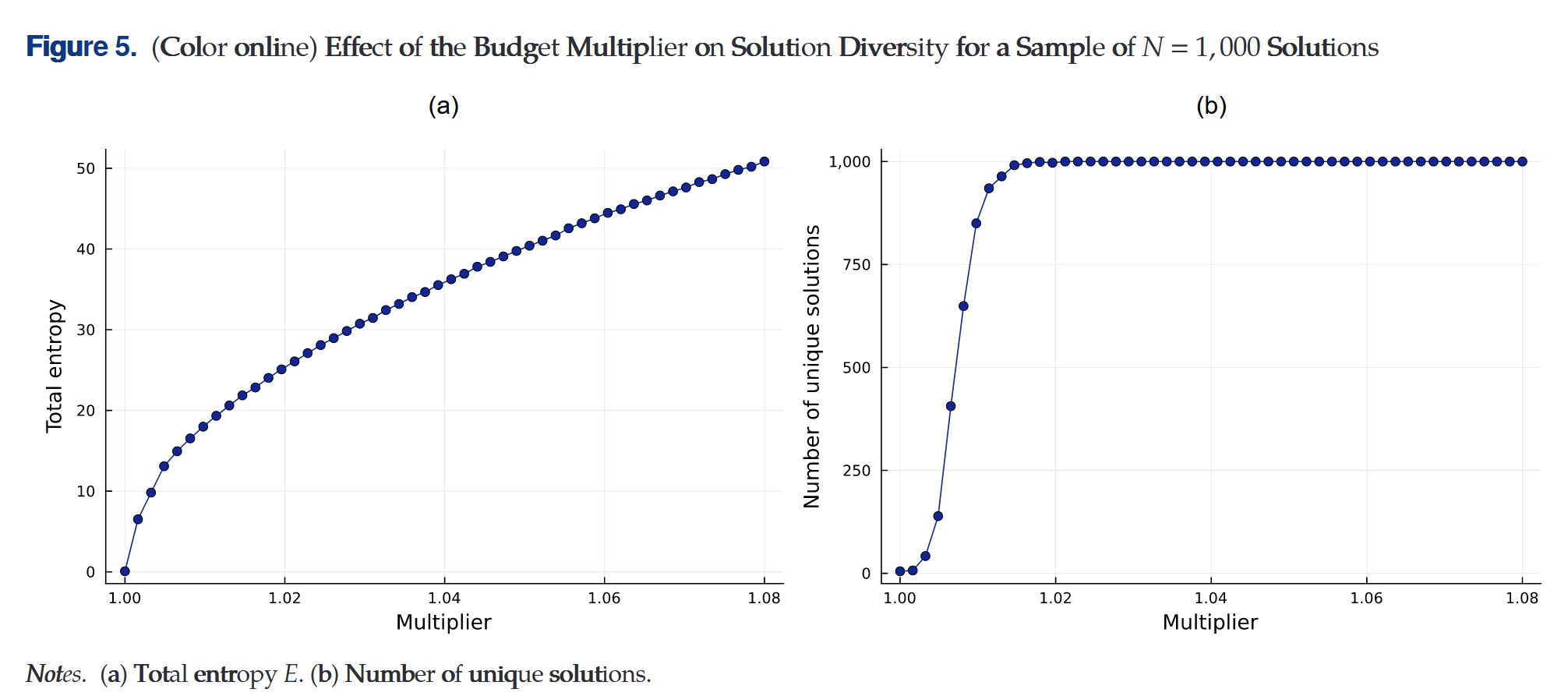
选择平衡解的质量与多样性的参数$\gamma$会是一个挑战，令$p(s,t)=\frac{1}{N}\sum_i\mathbf{1}_{H_{i,s}=h_t}$为学校$s$上课时间在抽样次优解中经验分布的概率质量函数，分布的香农熵为$e_s=-\sum_t p(s,t)\mathbf{ln} p(s,t)$，整体抽样解的香农熵为$E=\sum_{s=1}^S e_s$

实验表明$\gamma=2%$足够保证1000次抽样是独特的

交互UI设计

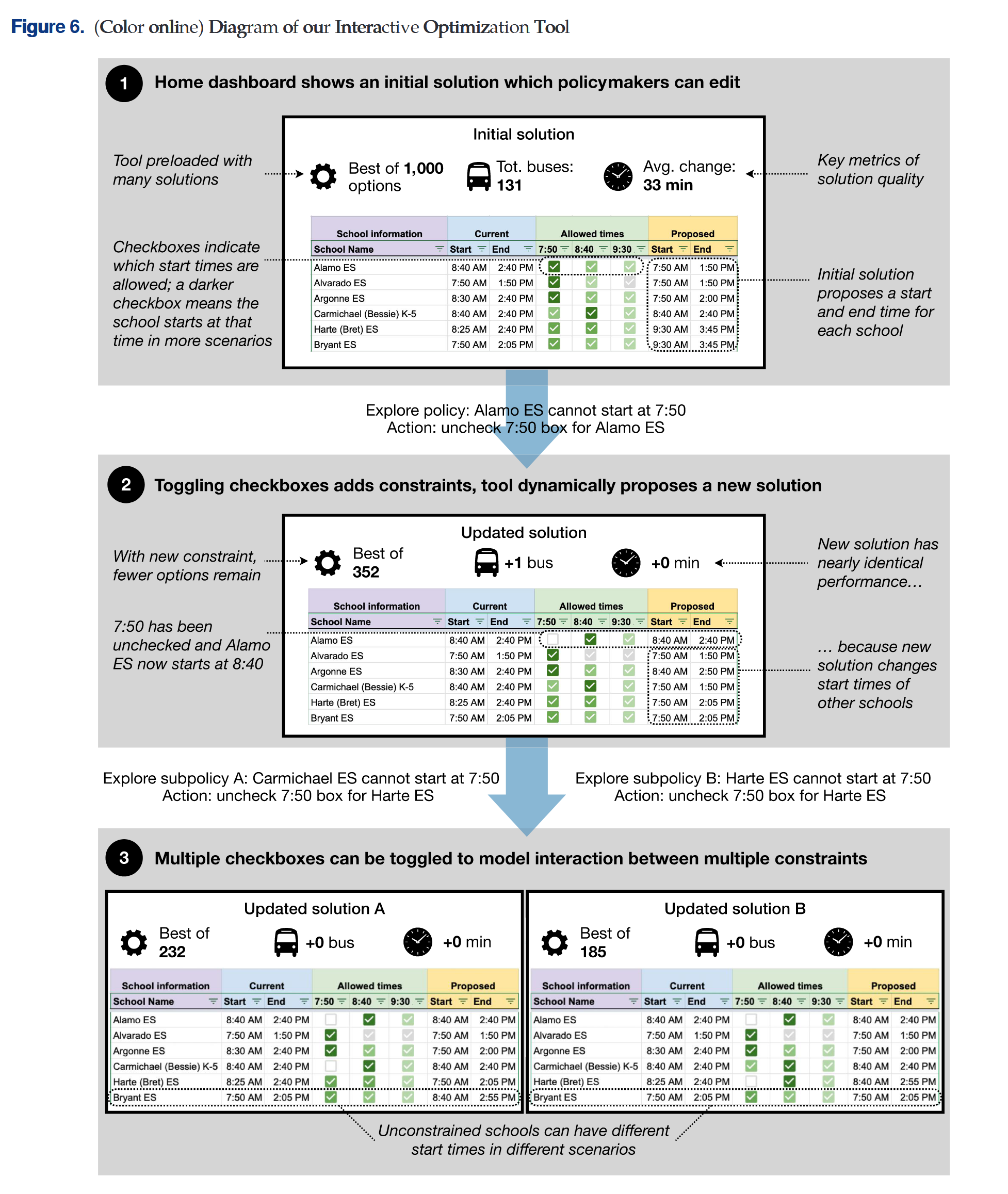
应用

将模型应用到学校的课表规划中，结果大同小异，不再赘述

Collaborative learning and decision making on pricing and recommendation: a simple framework for planning ²

Proxy-aided demand learning with an application to various pricing problems ³

• Previous
  【阅】本周阅读摘选2025-11-03 → 2025-11-09
• Next
  【阅】本周阅读摘选2025-11-17 → 2025-11-23